The model-less learning system (MFLC) can be used as a strategy to control processes such as the continuous agitated tank reactor (CSTR) and, in particular, the highly nonlinear Klatt-Engell bioreactor. MFLC schemes are being implemented in many industrial processes and are based on the reinforcement learning approach (RL) and have the following elements: states, actions and rewards, and elements of a Markov decision process problem (MDP). The term without model refers to the fact that the system does not use the transition probability matrix associated with the MDP. This represents a total ignorance of the environment (plant) with only available information of states, actions and rewards. The RL is based on the method outside the policy in which the policy is continuously improved until it is optimal using the Q-learning algorithm.
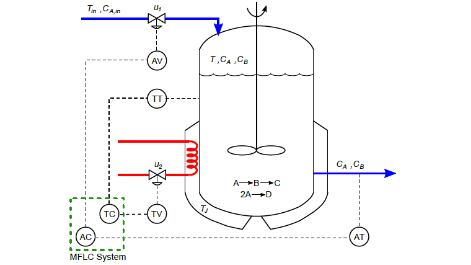
The MFLC scheme consists of the following blocks: status, policy, action value function and control signal estimation. States are defined at different error intervals, actions are a sequence of control signals and the reward function determines the penalty or reward for actions. It is a reward if the state gets zero errors and it is a punishment if there is a mistake. The situation block finds the status and calculates the reward. The action value function block provides the value of performing an action in a specific state when following a policy calculated by the Q-learning algorithm. The policy block chooses the best action based on the information stored in table Q. The control signal calculation block is a linear equation that evaluates the action value (selected by the policy) and determines the actuator control signal. A training process is required before applying the MFLC scheme to the plant and requires an exploration-exploitation mechanism based on the ϵ-greedy algorithm. By completing the training process, you get an optimized Q-table with your optimized policy. The MFLC scheme consists of two independent MFLC controllers applied to the bioreactor (Fig. 1). The structure of the control system is presented in Fig. 2.
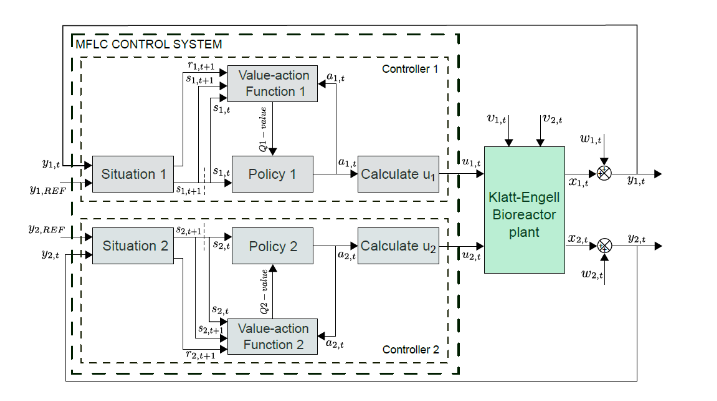
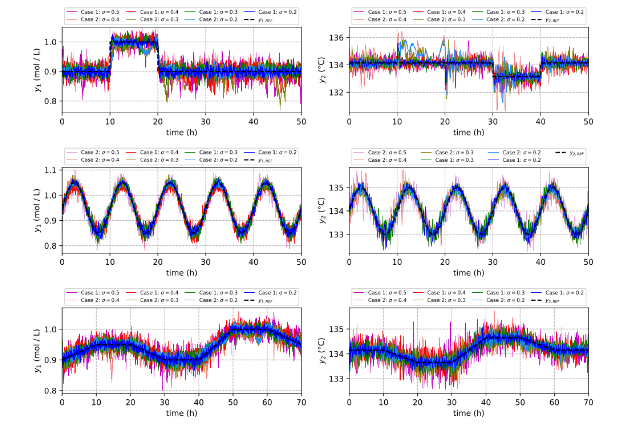
Fig.3 shows the good performance of the MFLC scheme using 3 different references while adding a high level of Gaussian noise signals to the output variables of a nonlinear bioreactor. The results show that the RL scheme is capable of handling high noise levels and could be applied to other industrial processes with non-linear dynamic behaviour. The MFLC scheme has the advantage of working with non-linear environments using only information from control signals and output variables. The voracious algorithm is very important for finding optimal values; however, the choice of the correct control elements and parameter values depend on the experience of the RL practitioner.