El sistema de aprendizaje sin modelo (MFLC) se puede utilizar como una estrategia para controlar procesos como el reactor continuo de tanque agitado (CSTR) y, en particular, el biorreactor Klatt-Engell altamente no lineal. Los esquemas MFLC se están implementando en muchos procesos industriales y se basa en el enfoque de aprendizaje por refuerzo (RL) y tiene los siguientes elementos: los estados, acciones y recompensas, y los elementos de un problema de proceso de decisión de Markov (MDP). El término sin modelo se refiere al hecho de que el sistema no utiliza la matriz de probabilidad de transición asociada con el MDP. Esto representa un desconocimiento total del entorno (planta) con solo información disponible de los estados, acciones y recompensas. El RL se basa en el método fuera de la política en el que la política se mejora continuamente hasta que sea óptima utilizando el algoritmo Q-learning .

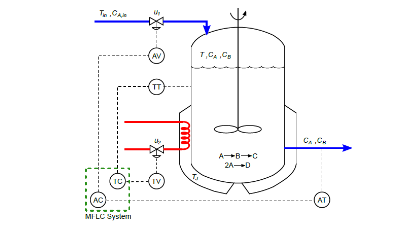
El esquema MFLC consta de los siguientes bloques: estado, política, función de valor de acción y estimación de señal de control. Los estados se definen en diferentes intervalos de error, las acciones son una secuencia de señales de control y la función de recompensa determina la penalización o recompensa por las acciones. Es una recompensa si el estado obtiene cero errores y es un castigo si hay un error. El bloque de situación encuentra el estado y calcula la recompensa. El bloque de funciones de valor de acción proporciona el valor de realizar una acción en un estado específico cuando se sigue una política calculada por el algoritmo Q-learning. El bloque de políticas elige la mejor acción en función de la información almacenada en la tabla Q. El bloque de cálculo de la señal de control es una ecuación lineal que evalúa el valor de la acción (seleccionada por la política) y determina la señal de control del actuador. Se requiere un proceso de entrenamiento antes de aplicar el esquema MFLC a la planta y requiere un mecanismo de exploración-explotación basado en el algoritmo ϵ-greedy. Terminando el proceso de entrenamiento, se obtiene una tabla Q optimizada con su política optimizada. El esquema MFLC consta de dos controladores MFLC independientes aplicados al biorreactor (Fig. 1). La estructura del sistema de control se presenta en la Fig. 2.

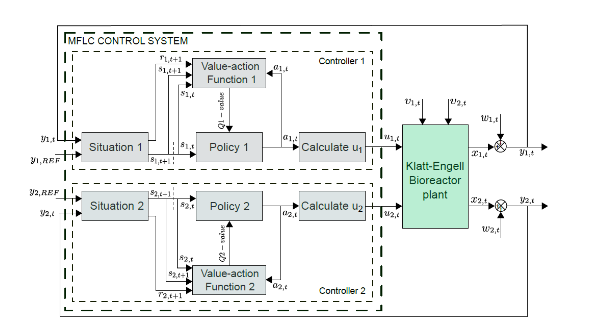
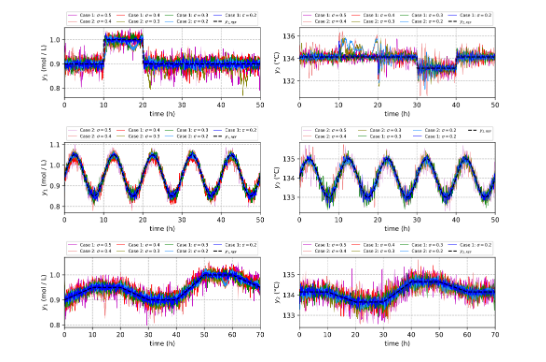
En la Fig.3 se muestra el buen desempeño del esquema MFLC utilizando 3 referencias diferentes mientras se agrega un alto nivel de señales de ruido gaussiano a las variables de salida de un biorreactor no lineal. Los resultados muestran que el esquema RL es capaz de manejar altos niveles de ruido y podría aplicarse a otros procesos industriales con comportamiento dinámico no lineal. El esquema MFLC tiene la ventaja de trabajar con entornos no lineales utilizando únicamente la información de las señales de control y las variables de salida. El algoritmo voraz es muy importante para encontrar los valores óptimos; sin embargo, la elección de los elementos de control correctos y los valores de los parámetros dependen de la experiencia del practicante de RL.

Actualmente profesores de Bioingeniería de UTEC se encuentran trabajando en proyectos similares. Si estás interesado en ser parte de proyectos similares que esperas: ¡Únete a  Bioingeniería de la UTEC!

References:

1. L. L. Estrada-Rayme and P. Cárdenas-Lizana, «A Noise-Insensitive Reinforcement Learning Control for a Nonlinear Bioreactor,» 2022 IEEE XXIX International Conference on Electronics, Electrical Engineering and Computing (INTERCON), 2022, pp. 1-4, doi: 10.1109/INTERCON55795.2022.9870085.
2. L. Estrada-Rayme and P. Cárdenas-Lizana, ”Model-Free Learning Control of a Nonlinear CSTR system”, 2021 IEEE XXVIII International Conference on Electronics, Electrical Engineering and Computing (INTERCON), 2021, pp. 1-4, doi: 10.1109/INTER- CON52678.2021.9532890.
3. L. L. E. Rayme and P. A. C. Lizana, ”Control System based on Reinforcement Learning applied to a Klatt-Engell Reactor”, 2020 International Conference on Mechatronics, Electronics and Automotive Engineering (ICMEAE), 2020, pp. 92-97, doi: 10.1109/ICMEAE51770.2020.00023.
4. S. Syafiie, F. Tadeo, E. Martinez, ”Model-free learning control of neutralization processes using reinforcement learning”, Engineering Ap- plications of Artificial Intelligence, Volume 20, Issue 6, 2007, Pages 767- 782, ISSN 0952-1976, https://doi.org/10.1016/j.engappai.2006.10.009.
5. S. Syafiie, F. Tadeo, E. Martinez, T. Alvarez, ”Model-free control based on reinforcement learning for a wastewater treatment problem”, Applied Soft Computing, Volume 11, Issue 1, 2011, Pages 73-82, ISSN 1568- 4946, https://doi.org/10.1016/j.asoc.2009.10.018.
6. Uçak, K. ”A Runge–Kutta neural network-based control method for nonlinear MIMO systems”. Soft Comput 23, 7769–7803 (2019). https://doi.org/10.1007/s00500-018-3405-5.

Otros posts